足し算
2019.01.23(since2017.1.8)
サイトマップ 、トップ << 電よも < <
１ビットの加算器を考えてみましょうか。 単純にA,Bの加算だけ実行する２入力のハーフアダー（２ビット入力）と、下位からの繰り上がり対応も行うフルアダー（３ビット入力）が存在します。それぞれ、出力Zと、次段への繰り上がり（Co)の２出力を持っています。
排他的論理和（エクスクルシブオア）を使うと、結構簡単に論理回路かけるのですが、排他的論理和というのが結構難しい回路。 設計課にいると他社特許調査の名目で公開された特許の抜粋が回ってきますが、どこの会社もこの論理回路を考えるようで、時折関連特許を見かけることがあります。そんなわけで、排他的論理和を使わずに、論理回路を書いてみましょう。
その前に、CMOSゲートは、基本論理反転ゲートです。PMOSトランジスタは、ゲート入力がLになると、出力ドレインは電源Hに接続されるソースに接続されます。NMOSは入力ゲートがHになると出力ドレインはやはりグランドLに接続されるソースと導通します。一般にはソースが、単純にソースにつながるか、他トランジスタのドレインにつながるかにより、直並列回路の組み合わせになります。
したがって、ANDゲートではなく、NAND,ORテートではなくNANDを使うのが気持ち良い。どんな回路にするかドモルガンの法則の使い方がその人のセンスになって表れてきます。 以下の回路は現役離れて長いので、期待されるような回路ではありません。 クロックドCMOSという回路を使うと実はすっきりした回路になる事がありますが、特許に引っかかる可能性あるし、LSI内部設計以外に汎用部品として一般に使えるわけでは無いので、の気が付かなかったことにします。
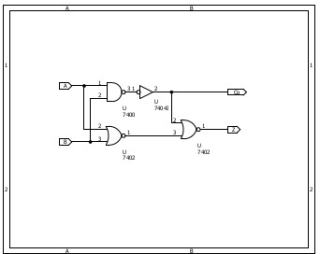
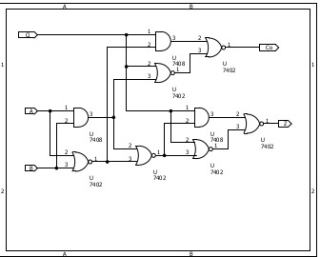
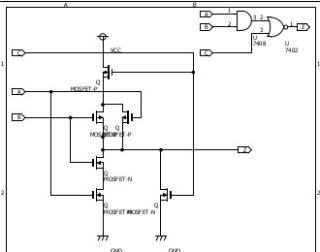
ちなみに、２入力ANDが、NORゲートの１方に入力される３入力の回路（ANDNORと呼ばれるのかな？）は、普通に論理回路を並べると、NAND+INV→NOR入力という形になります（もっとも、ANDは、ANDゲートとして内部接続したゲートが用意されるのが普通でしょう（これらの方法では面積はともかく１０トランジス回路です）。 しかし、トランジスタ回路を書く人はちょっとパズルします。パズルの結果は６トランジスタで実現可能。直列２トランジスタが律速するとはいえ、一般回路の３段ゲートよりはましでしょう（NORやNANDも高速変化は１トランジスタですが、低速変化側は２トランジスタ直列なので、このような回路より優れています）。 回路設計だと、PMOSとNMOSが同性能ではない（NMOSの方が比較的高速）などを織り込んで最終回路を書いてゆきます。それをいうと、上記フルアダーはNORゲート４段直列回路なので、及第点はとれませんねぇ。
フルアダーをつなげて４ビット加算器を作ってみましょう。下位の繰り上がり出力Coを、上位の繰り上がり入力Ciに接続してつなぎます。
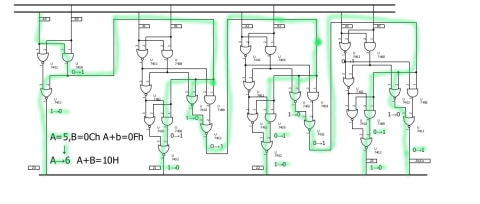
それほど確定速度を要求しないのであれば、上記のとおりで問題ありませんが、上の図に示したように、下位の変化は、順番に上位の値や、さらに上位向けの繰り上がりに影響を与えます。 デイジーチェーンとよんで数珠繋ぎのパスが、回路の律速となります。
これを対処するために、キャリールックアヘッドと呼ばれる繰り上がりを高速化するアイデアが、いろいろ考案されています。 論文か先例を参照に大規模システム開発の課程で、大先輩が論理設計失敗して、数日分の作業がふいになった悲しい過去がありました。まあ、サインオフ前に見つかったので良しとしよう。 加算器であっても、繰り上がりの高速化というのは複雑な問題を抱えています。
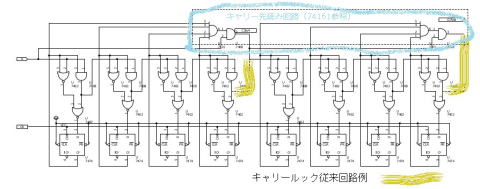
下記は74LS161/2/3/4等の、４ビットカウンタ―に内蔵されている（とカタログに記載の）回路を使ったカウンタのキャリー先読み回路。
上記回路の例だと、下位ビットから順番に確定しないと、上位が確定しないので、動作時間に制限がかかる。 下記の回路では、４ビットがallHの場合（0Fh)の場合に、下位からキャリー命令が入れば、all０になって、繰り上がり信号を出すことになる。 これを条件にキャリー信号を作っています。
これによって、８ビット分のデイジーチェーンではなく、４ビットデイジーチェーンの動作で８ビットともに動作確定できます。 これらのカウンターにキャリー入力（カウントイネーブル）が２系列あるのは、複数段カウントするための加速回路運用のためです。 昔の本だと、２つのカウントイネーブルの使い分け（外付け回路例）が出ていましたが、加速という原理を勉強するのに、探してみるといいかと思いますよ。
カウンターは、＋１だけ（デクリメントカウンタもあるけど）なので、上記のような簡単なキャリー高速化回路ができますが、フルアダーの場合、条件が難しいので、一筋縄ではいかない困難なものだと理解してください。 画期的なアイデア見つかったら特許物ですよ。
(2019.01.23)ちなみに、ヤフー知恵袋にて、フルアダーの話題がでたので、ちょっと、回路の対称性について、意見を述べてみた。
--------------------------------
フルアダーの、A入力と、B入力と、C(in)入力は、真理値表上同じ扱いなんやで。真理値表書いて確認してみ（２つの加算じゃなく、３bit入力の加算器と考えてええんやで）。
実際等価か？というと、ken********さんの図に示されるように、下位ビットのC(out)が、次の段のC(in)につながって、その出力C(out)が、次のC（in)につながるように、数珠つなぎになってるでしょ？ 例えば３ビットで、001+111の場合、最下位の繰り上がりが、２ビット目に加算されて、最初繰り上がりないかなぁとおもったら、やっぱり、そこで初めて、最終段に繰り上がりが発生するでしょ？ 回路の律速（もっとも遅い経路）が、これになるわけさ。
でもって、何とか、C(in)からC(out)への伝搬が早くなるように回路を作りたいなぁと思うのが、回路設計者の主題。だから、真理値表上同じでも、むやみに適当につなげないようにする方がええと思うんや（どうせ十分早いから、おんなじじゃという意見もあり。ええなぁパワーユーザが使えるものは．．．）まあ、A入力とB入力違うんかい？というと、たぶん区別ないんやけどね。細かいこというと、例えば２入力NANDゲートの回路は、NMOSは、直列２段接続なんだけど、どっちのトランジスタがソース側（GND）かどっちがドレイン（出力信号）側かで、微妙に違うという話がないわけでもない。昔々SPICE結果をもとに、職場の先輩にレクチャ受けた記憶があるが、実際違うんか？というと、わからんねぇ
まあ、千里の道も一歩からやから、今十分考えておくんやで。
------------
サイトマップ 、トップ << 電よも < <