(since2019.11.08)
サイトマップ 、トップ << 電よも < <*
はてさて、円周率ってなんやろか?
小学校でならったのは、直径*パイ=円周長。 LPレコード(EPだったかな?)を家からもちよって、机の上で転がして巻き尺(?)で円周をはかって、同様に直径も物差しではかって、机隣り合わせの二人組で円周率を計算するという算数の授業がありました。
ミリ以下を目視で読み取って、計算すると3.14ぴったりに割り切れて、近所のグループより円周率に近いと喜んでたら、先生に、3.14159..と割り切れない端数があるので、3.14で割り切れたのは正確じゃ無いといじめられました。
知恵袋で円周率の求め方という質問がたっていて、ひねくれ者は級数展開による方法じゃなく、乱数利用のモンテカルロ法というのを紹介。興味はもってもらえなかったけど、懐かしいので、試しに計算してみましょうか。
その前に、3月14日は円周率の日とのこと。円周率: π ≈ 3.1415926535898...のうち、653までは暗記。その後5898が出てくるときと、5989だったかな?と迷うこととあって、まあ覚えているうちには入りませんね。
昔は、
身一つ世一つ生くに無意味 曰く泣く身に宮城(みやしろ)に虫散々闇に泣く
最近だと、
産医師異国に向こう 産後薬なく産に産婆四郎次郎死産 産婆産に泣く 御礼には早よ行くな
と覚えるんやそうな。そんな桁数いらんがな
1)面積比 仮に計算した結果をブログに示しました。.
学生時代8bitPCの走り(当時マイコンと呼ぶ)の、市販デモソフト(アスキー出版の書籍で、プログラムを収めたカセットテープも別売)に、N-BASICによる例がでてたのを覚えています。同じく知恵袋で、10進BASICというフリー言語の紹介してもらったので、ためして見ました。
半径1の円の面積は、1*1*パイ=パイ
この円の外接正方形の面積は、一本が2なので、4。
つまりこの面積比を求めれば、4:パイという数値が求まる。
円の面積を求めるのに、パイを使うのは論外なので、どうやって求めればいいか?
モンテカルロ法というのは、乱数で、XYの2点の座標を決めて、これが、X^2+Y^2=1の半径1の円の中に入るかどうかで、判断しました。
つまりBASICの乱数が0~1の範囲の乱数なので、XYがともに0~1の、1/4面積の円を想定して、円の中か外かを求め、これが面積比に比例するという判断をするわけです。確率を4倍すればパイになります。
RANDOMIZE
DIM ref(10)
SET WINDOW 0,1000,0.01,-0.01
SET POINT STYLE 2
SET POINT COLOR 2
DRAW AXES0
FOR i=1 TO 1000000
LET x=RND*2-1
LET y=RND*2-1
IF x^2+y^2 =<1 THEN LET en=en+1
LET ref(MOD(i,10)+1)=en/i*4
PLOT POINTS: i/1000,en/i*4-PI
NEXT i
FOR j=1 TO 10
PRINT ref(j)
NEXT j
END
100万回リピードで最後の10回は
3.14284828563457
3.14284514276114
3.142845999922
3.14284685708114
3.14284771423857
3.14284457137829
3.14284542853629
3.14284628569257
3.14284714284714
変化をみると数十万回平均すれば、そこそこの数値化も

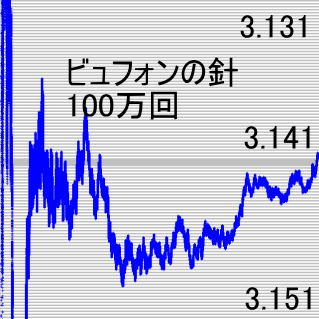
2)ビュフォンの針実験法
知恵袋で雑談でモンテカルロ法でπを求めてみたといったら、モンテカルロ法って針をなげるんですよね?と話がかみ合わない。いろいろ教えてもらうと、フランスの物理学者ビュフォン氏が、間隔dの罫線を引いた紙の上に、長さd/2の針を投げて、罫線に針が引っかかる確率を求めて、その確率の逆数が円周率だという説を唱えたとのこと。
間隔dの罫線とか、まっすぐな針を投げるという行為のどこに円周率がでてくるんや?不思議な理論ですよね。 話を聞くとすごく面白い。
罫線に対して、投げた針との角度は一様ですよね?ランダムに変わる。
横軸を、角度0~90度(π/2)とする。縦軸は、その角度で、針が罫線に触れる範囲(位置範囲:0点から、d/2の距離)。角度は、90~180度は単に反転だし、180~360度も、0から180ど対象。つまり0~90度だけ考えて確率を求めればよい。間隔も0~D/2と、一本上の罫線に対するD/2~Dの範囲は対照なので、これも代表例だけ考えればよい。
0度:針が罫線上以外は触れないので仮想確率0。
90度:針の長さと間隔同じD/2なので、どこでもokつまり確率100%
45度:D/2*sin(45)<位置 なら触れる。
つまり、確率は D/2*sin(θ)
θをパラメータとして、確率はsin波のπ/2の積分となる。
確率=∫高さ*sin(θ)dθ atθ=0~90度
=D/2*π
シミュレーションは、この中点ベースではなく、(0,0)-(1,1)の範囲で、乱数により始点(x1)と傾きθを決め、X1=0ならカウント。0<X2=X1+0.5sin(θ)<1以外をカウントするプログラムにした。理由は乱数が0~1で発生するからという単純な理由。
RANDOMIZE
DIM ref(10)
let sizwin=1000
SET WINDOW 0,sizwin,0.01,-0.01
SET POINT STYLE 2
SET POINT COLOR 2
DRAW grid
DRAW axes0
OPTION ANGLE DEGREES
LET en=0
LET rep = 1000000
FOR i=1 TO rep
LET ok=0
LET X1=RND
LET S=360*RND
LET x2=x1+0.5*SIN(s)
IF x1=0 THEN LET ok=1
IF x2<=0 THEN LET ok=1
IF x2>=1 THEN LET ok=1
LET en=en+ok
IF en>1 THEN LET ref(MOD(i,10)+1)= i/en
IF en>1 THEN PLOT POINTS: i/(rep/sizwin),ref(MOD(i,10)+1)-PI
NEXT i
FOR j=1 TO 10
PRINT ref(j),ref(j)-PI
NEXT j
END
100万回リピートの結果
3.14143438811672 -1.58265473071696E-4
3.14143752984643 -1.55123743360987E-4
3.14143080204966 -1.61851540135215E-4
3.1414339437695 -1.5870982029494E-4
3.14142721600513 -1.65437584665968E-4
3.1414303577151 -1.62295874696065E-4
3.14142362998313 -1.69023606664168E-4
3.14142677168323 -1.65881906564576E-4
3.14142991338333 -1.62740206464984E-4
3.14142318567389 -1.69467915900684E-4
一般的な面積法と比べると収束性悪い。 が、針を投げるだけで円周率が求まるという発想に拍手。