インピーダンス（交流抵抗）

2017.1.4
サイトマップ 、トップ 　<< Z < <　 インピーダンス

直流と同じで、インピーダンス：Z=V/Iで求まります。　三和テスターオプションのCL-22ADという電流クランプを持っています。一時期電力素子制御に関わる仕事をしたので、試しに１０A程度の電流を測れるものを購入してみました（定格は２００A　ＤＣ／ＡＣ（～400Hz)という品物。
これで電子回路を測るのはちとオーダが違いすぎる。　オシロでみるのが目標だけれど、1mV/Aの出力感度では、ちと難題。クランプの周りを１００回巻きすると、何とか、波形が見える気がするので、１００倍ゲインの増幅器を作ろうとしたが、ノイズの問題もあって、断念。４００Hzまでといわれると汎用性という意味でも断念が正しいかな？　ちなみに、１００回巻きすると起電力が１００倍になるというのは、ファラデーさんが教えてくれました。

しかたないので、被測定物と、直列抵抗をいれて、交流電圧の出力電圧を調整して、被測定物に一定電圧を印可して、直列抵抗の電圧から電流値を求めることにします。

１．直列抵抗

(１ｋΩの)被測定物に、電流測定用１ｋΩの抵抗を直列接続し、被測定物に約１Vppかかる用にSGの電圧調整し、測定条件とした。

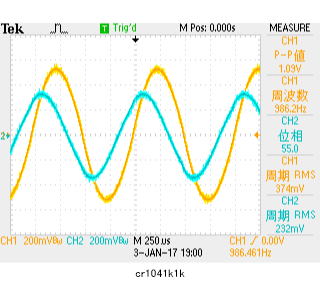
以下ｃｈ１（黄色）が、被測定物（本件では１ｋΩ抵抗）の両端の波形１Vｐｐ目標であるが、SGの精度の問題があって、０．９Vなのは、ご勘弁。
ｃｈ２（水色）が電流測定用抵抗（本件は１ｋΩ抵抗）の両端の電圧。両抵抗の接続点をオシロGNDとして、それぞれ逆側の電圧をみている。電流の流れる方向の定義を合せるために、ch2は反転表示としている。

左は通常のYTモード：要するに横軸は時間。縦軸は電圧です。　右は、XYプロット（リサージュという名前が解りやすいかな？）縦軸がch2電圧軸、横軸はch1電圧軸（横軸が印可電圧、縦軸は素子に流れた電流（に比例：電圧を1kΩという抵抗値で割ったらmA単位に）。

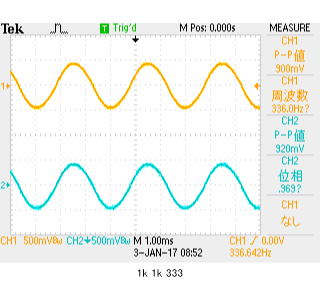
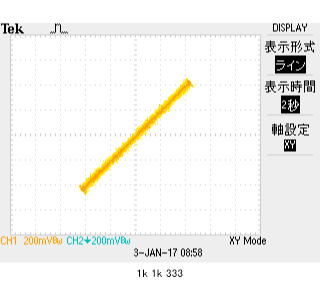
結果：　900mV印可したところ、電流は直列抵抗１ｋΩに920mV発生したことから、0.982/1k(A)流れている。したがって、被測定物はZ=0.9/(0.92/1k)≒980Ω（期待値1kΩ）と、測定誤差の範囲でしょう。　ちなみに、３項目測定値ch2位相というのは、入力電圧位相と、電流位相が、ほぼ同位相（１度弱ずれの測定誤差）を示している。　したがって、リサージュ波形は、右上がり傾き45度のほぼ理論通りとなることを示している。

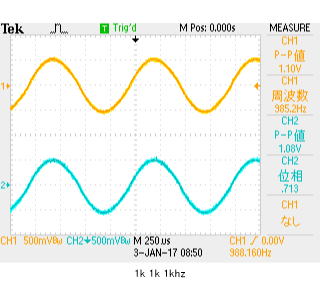
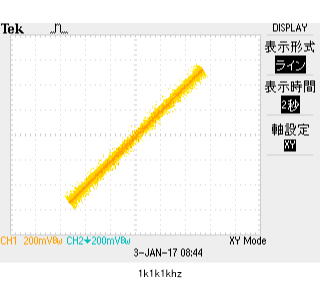
今度は入力正弦波を、333Hzから、１ｋHzにあげたときの関係。　測定誤差の範囲で、周波数変えても、同じであるといえる。

２．コンデンサ

表示104の積層セラミックコンデンサを測定してみた。　三和テスターPC101での測定容量は、149nF。　
|Z|=1/|ωC|から算出すると、3.2kΩ@333Hz／１Ω@1kHzとなる。電流測定用抵抗は、１kΩにする。

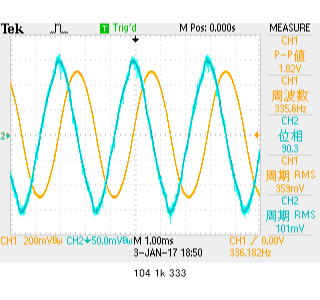
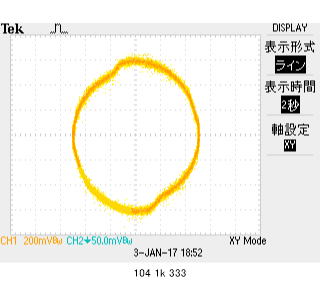
333Hz駆動でのオシロ計測値からインピーダンスを求めると、Z=0.353/(0.101/1k)=3.50kΩ　位相差約90度。　プラス表示なので、波形が進む（ch2の電流相当が、ch1電圧に対して位相が進む）事を示しています。　リサージュは円になります(つぶれ気味ではありますが、傾いていないのが注目ポイント。リサージュが円になるのは±９０の場合ですが、区別はつかないけれど、定性的に正しい測定ができていることがわかる。絶対値誤差１割はいただけないかな？　まあ、テスターで測るコンデンサ容量が正しいわけでもなかろう（100ｎスペックで実測150nは正しいのだろうか？）

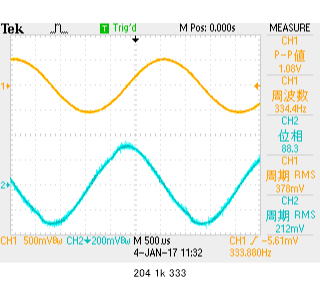
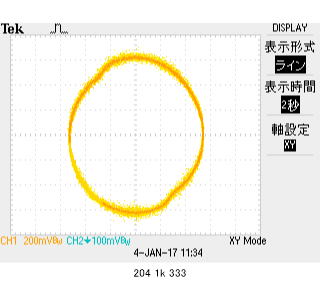
同周波数において、同一仕様コンデンサを２個並列にして、容量２倍(PC101によると293nF：ほぼ2倍）にしました。この時のインピーダンスは、Z=0.353/(.212/1k)=1.77kΩ。
先の計測の3.50kからほぼ1/2になる事がわかります。

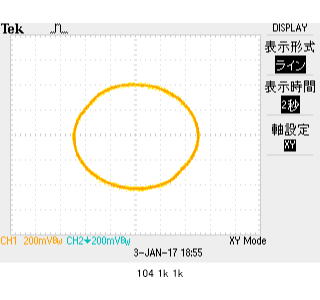
1ｋHz駆動でのオシロ計測値からインピーダンスを求めると、Z=0.354/(0.288/1k)=1.23kΩ。　位相は+９0度のまま、周波数が３倍になると、抵抗値が１／３になることが、理解できたでしょうか？
先のコンデンサの容量が２倍になると、インピーダンスが１／２になる。周波数が３倍になると、インピーダンスが１／３になるという測定結果は、コンデンサのインピーダンスの公式　Zc＝1/jωC　を素直に表現していることが確認できました。

ところで、ここまでは、純粋に（コンデンサ・抵抗）に印可される電圧と、それによって直列抵抗に流れる電流を、独立測定していましたが、RC直列回路として、印可電圧と、電流の関係を見てみましょう。　交流抵抗値が偶然同等オーダで近いので（なおかつ数倍オーダで相違がある）、140nFと1kΩという前述測定につかったものを、そのまま利用します。

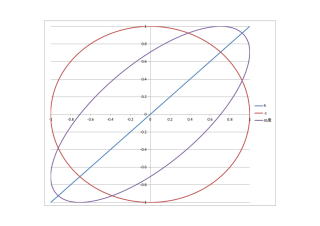
位相を考える。インピーダンスの逆数ベースで、位相を求めると、ArcTan(1.23/1)=50.9度　測定誤差を考えると、電圧電圧間の位相差５５度を表していると考えて良い。　リサージュに関して、振幅が等しくないので、歪がでているが、抵抗の０度位相、コンデンサの９０度位相に対して、中間の５０度を、感覚的に示しているのが解るかとおもう。　８ビットPC（NECPC8001）を購入した時、ASCII社がサンプルプログラム集を出版していましたがリサージュ表示プログラムがあって、X軸Y軸の関数（周期や位相も含む）を変えて遊んだのを思い出します。　今でも、エクセルで通常のグラフではなく、分散図でリサージュを作ると例えば奇数倍周期とかいろいろ面白いかもしれません。　下図は、電流電圧同位相のR測定時の原理（右上４５度直線がり）と、９０度位相のC測定時の円形、および、実軸・虚軸１：１（インピーダンスがそれぞれ等しいRC直列回路の）楕円を、分散図として表示したものです。電子工学演習ではなく、電気工学実習で、オシロのリサージュ波形を作るという課題があったのを思い出しました。

雑談：上で、コンデンサが、１．２ｋΩとか３.５ｋΩという単位で表しているのに、違和感を持った人いませんか？　コンデンサの単位は［Ｆ］ファラッドです。コンデンサ単体では確かにファラッドという単位で正しいですが、他の素子と一緒にインピーダンスという次元で話をするときに、Z=1/ωCという次元でΩという単位に統合するのが便利。　物理的に説明しろといわれるとちと困るんだけど、インピーダンスが周波数および周波数の逆数だということで比例定数が単純になるのが、今のファラッドという単位になるのかな？　コンデンサの容量はインピーダンスというアプローチ以外に物理の世界で面積に比例し、電極の間隔に逆比例して、電極間の詰め物の誘電率に比例するという別の求め方もあります。これもどこかの定数で（誘電率と比誘電率で）つじつま合せているんでしょう。

ちなみ、電子工学演習の小テストで、”コンデンサが１０Ωで、抵抗が１０オームで．．．”というような出題をみて、”コンデンサにΩという単位がついていますが、ファラッドの間違いですか？”という質問をした人がいましたが、教官から、インピーダンスの意味わかっていないだろう！と即座に却下されていました。次元という言葉よく考えましょうね。　物理現象を説明する方法（単位の定義すらいろいろある）は一つだけとは限りません。

次に、コイルも追加する予定。

--------------------------
サイトマップ 、トップ 　<< Z < <　インピーダンス