続エレキギター

2017.2.16
サイトマップ 、トップ 　<< Z < <　 ギター<

等価回路を、エクセルで簡単に評価してみる。

まず、元となるギターの原信号（モデル）を考える。

ギターは、ヘッドのつけ根のナット（あるいは指で押さえたフレッド）と、本体側ブリッジの間が半波振動するのが原則(両端が振動の節。弦の中点が腹になる)。　この半波振動に、高調波が重畳される（音色を決めるものやね）。　安定振動なら、この半波の整数倍の高調波が乗る。　つまり素直に、基本波の整数倍の高調波が乗ると考えられる。

ところで、弦の振動が左右非対称は美しくない。　２倍波はヘッドとボディ間が全波振動。すなわち弦の弦の中点両側を挟んで左右が逆位相で動く。この動きは基本波のセンタの腹の位置に対するぶれ成分になる。、ピックではじいた直後は盛大にあるとしても、急速に減衰すると考えられる。　エントロピーは増大し均質になるのが原則（え？熱力学関係ない？いや真理だとおもうぞ）。　つまり、偶数倍は消滅し、奇数波のみの高調波が安定波形と推定する。

振幅に関して、第０近似は、波長に比例するという話になるが、例えば、２倍波の腹にあたる１／４の位置は、基本波の４５度で傾き１／２。ブリッジからの距離が単純に１／２に近くなったこと以外に、これまで基本波の腹にあたるぶぶんは、むしろ、最大振幅方向に引っ張る力があったはずなのに、これがなくなり、さらに、２倍波の節になる（基本波の腹）方向から同じ力で引っ張られることになるので、すくなくても、３倍のちからで、引っ張られることになるので、相似ではなくさらに小さな振幅にならざる得ない。　さらに片持ちばね（例えばオルゴールのピン）の動作は剛性のワイパーなどの振動と異なり、たわみにより、先端の振動がより大きいことの配慮も必要となるかと思われる。即ち、１次関数ではなく、もっと複雑な関数関係。

位相に関して。弦の中央は、基本波のはらの最大振幅位置。ここに３倍波が重畳される場合に、はらの位置が、高調波の逆位相でへっこむというのは、美しくない。　すると、３倍波の真ん中の部分は、基本波と同位相なので、ブリッジ・ナットの付け根の部分は、逆位相になるのが正しいと思われる。　５倍波の場合は、やはり真ん中のブロックが基本波と同位相だとすると、両側のそれぞれ１波が、逆位相、正位相の半波のがつながり、ブリッジ・ナット部分で同位相が正しいと思われる。

ところで、フーリエの三角波は、上で推定した奇数倍波の合成であり、振幅は、周波数の２乗に反比例する事が知られている（振幅の４倍や、８倍に逆比例するとしても、√２に逆比例するとしてもそれらしい波形にならないが、二乗反比例なら、確かに三角波。　位相も、３，７，１１倍波が逆位相。５，９、１３．．ば同位相。　これを、ギターの安定した基本波形と考えることにする。

次にピックアップのｆ特の重畳。

回路モデルは前頁のものとする。　いやー、これがうまく解けない（物理的に納得する形にまとまらない）。　実部がマイナスになるとか、トーンコンボリューム０の場合に、２つのコンデンサの合成（単なる足し算）で、L,R,Cの直列回路相当にならねばならないとか。トーンコンボリューム最大（∞の仮定）で、LRC直列回路相当とか。ボリュームが中間（実定数最大含む）の場合に値が減少すれば、Cが大きくなるという定性的な推定の式にまとまるまで、四苦八苦。　いや回路解析の腕が落ちたもんだ。 このページ書き始めたのが2/10.　エクセル上の計算できるようになるのに、今日までかかってもた（もちろんこれだけやってたわけでは無いと言い訳しておく）。

前述LTSPICEの特性解析（右に採掲）とほぼ同等とみて良いと思う。　任意のゲインや位相が求まると、エクセルで任意波形の特性が見えるのが今回の注目ポイントです(スパイスだって、代表的な波形入力できますが、帯域制限した波形とかいれるのに、数値ではなくLPFでも回路入れるほうが楽だったりして、まあ、ようとにより使い分けるのがいいんです。

トーンコントロールは、最初単純なローバスフィルタと思ったが、実際に、高域のカットから、中域を強調ることまで、イメージ通りのトーンコントロールが実行されているのが判る。　Cと、CR直列の並列回路って、ここだけｆ特など特徴が解りやすいい等価回路に直す書くのがこれほど難しいとは思いもしなかった。　ここでいう中域は、高域弦１弦の、１２フレッドを抑えたあたりの帯域。　４弦２フレッドを抑えたE（ミ）の３倍高調波あたりの周波数。

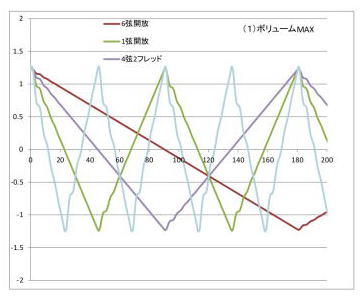
ｆ特の（１）のトーンコントロールボリューム最大（トーンコントロールスルー）状態の推定波形。　フーリエ変換した三角波（正弦波の和）をつかい、それぞれの周波数の正弦波に対して、前述フィルタ特性のゲインと、位相をそれぞれ加味して、人が普通に聞こえるという２０ｋHzまで加算したもの。　単純三角波ではなく、ｆ特の持ち上がった部分の数ｋHzの高調波成分が強調されて、波形が歪んでいる。　でもそれが、それらしいギター波形と思わない？　整数倍周波数が考えやすいので、６弦開放のミ。４弦２フレッドのミ、１弦開放のミ、１弦12フレッドを押さえたミの、４オクターブのミを選んだ。　高音の方が６ｋあたりの特異点に近い（減衰が少ない）ので、より歪が大きい。ｆ特図には、ドミソの逓倍波周波数をポイントとして記載しているので、オクターブ単位で、強調されるバンド幅の推定にご利用ください。

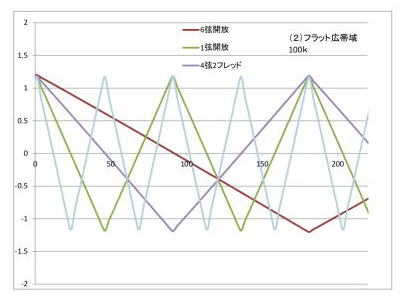
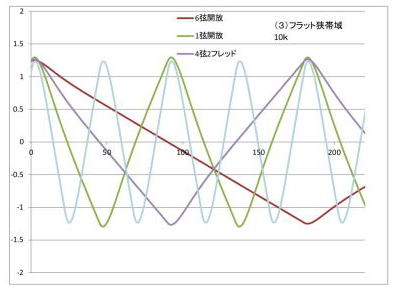
トーンコントロールボリュームを少し絞って、周波数的に特徴のあるピークのない素直なローパスフィルターで帯域の一番広いところ（シュミレーション上推定値100ｋΩ）の（２）左側の：高周波まで伸びているところと、　シミュレーション１０ｋΩのフラットの部分が一番狭い上一番狭い右図。　共に原信号と想定した三角波が素直に再現される。　ピュアオーディオの人にとっては、一番美しい波形かな。　右の周波数帯域が狭い方は、すなおに高周波成分がおとされて、三角波の頂点が丸くなっているのが判る。

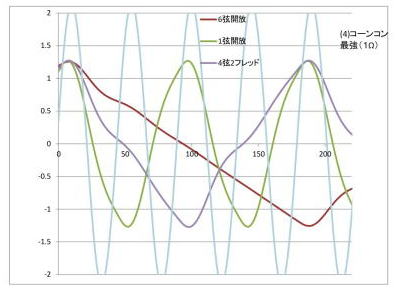
トーンコントロールの一番特徴的なポイント（ボリューム最小）のｆ特図（４）の部分。　周波数特性の肩：上限は、上記（２）、（３）と大差ないが、減衰率が高いことと、ｆ特上強調される周波数帯が発生する。　基本波の4倍波（存在しない偶数波）が強調される６弦開放は影響少ないとはいえ、基本波が、強調される１弦１２フレッドの場合は、音圧としても強調されているのが、見て取れる。　確かに、トーンコントロールとして、音が変わる。

パッと目は、単純ローパスフィルターかと思ったけど、いろいろ教えてもらった回路でした。　簡単にわかるスパイスというソフトは素晴らしい。

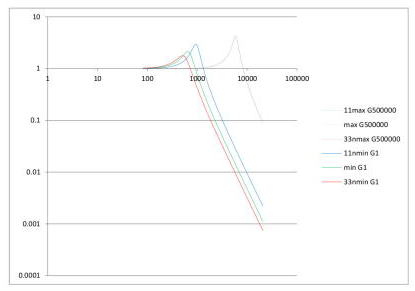
トーンコン用コンデンサの値を変えると、共振周波数が当然変わるので、同じ音を出しても、増幅率はかなり変わる（ピーク周波数付近の音なら）。
さらに、位相特性も変わるので、オクターブ違いの２重奏で、この近傍の位相がかなりずれるのが見て取れる。　振幅以外にあるいはこの位相差というのも音色に影響ある（位相特性聞いても判らんという噂も聞いた気がするが）。　倍半分でこの程度の差なので、数％程度だとすると、もともと大差ないかもしれないね。

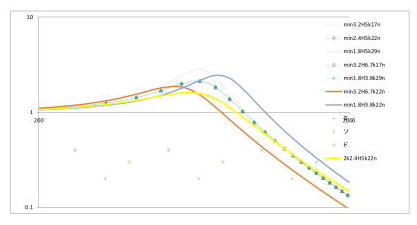
ところで、ピックアップを交換するとき、DC抵抗値が大きいものが良いものだ！！という迷信があるとか。
一般論として電子回路屋さんは、抵抗値が大きいコイルとは、内部R損失が大きい劣った部品というイメージを持ちます。LC共振回路を作っても、共振Qが低いので、ピーク感度が上がらないとか。
内部DC抵抗が高い方が良い例を考える。
１）Qが下がるので、ピーク感度が低く、それほど目立った強調されないので、むしろ聞きやすい。　これだと、単にトーンコントロールのボリュームを
大きくするのと大差ない（微妙に共振周波数がずれるはずだが、検出できるような差異ではない。上図の黄色が、トーンコンを下げた状況。
２）抵抗値が大きい→コイルが長い→Lの値が大きい。　これだと、共振周波数が下がるのと、ピーく感度が下がるのとが並列。　これって、おとなしくなるだけなので、メリットと考えるのがおかしい。　さらに、Lが変わった分、外付けCの値を変えて、共振周波数を同じにすると、まったく等価。
３）製品ばらつきで共振周波数がずれたのが、偶然心地よいだけ？　というのが最もありそうな気がする。　これも現物調査でないと結論出そうにないですねぇ

----------------------------------
サイトマップ 、トップ　<< Z < <　ギター<