世界の名作推理パズル100
2018.09.24(since2018.03.19)
サイトマップ 、トップ <*> (熊さんの色は , 変な立体)
(2018.04.26)本屋でタイトル見て面白そうなので、Newtonライト”辛口すうがくパズル”を購入。持って帰って奥付みたら、タイトル図書と同じ作者が、初出記事へのご協力者として筆頭に挙がってました。 あれ?パズル界の巨匠だったりしたのね!!
別ページでニュートンの悪口もどき発言したので謝罪の意味で興味がわいたら、なるだけ購入しています。 モンテカルロ問題取り上げていたのを見つけて、Newtonライト”確率のきほん”と一緒に購入してみました。
----------since2018.03.19-----------
よそでもちょっと話題に挙げた本(大学の先生の専門外?の趣味の本?)ですが、面白い本なので、ここにまとめて紹介します。
そもそも、何気なく本屋で手に取って、第一問考えたけどひとつ条件がたりない気がして、回答ページ読んだらまるで違うアプローチだったので、きちんと読むために購入した本です。
よくわからん(たぶん間違いのある第一問)はこの後論議したいと思いますが、結構面白いので、お勧めします。小学校のころ読んだ(タイトル思い出せない)パズルの本で見た問題がいっぱい取り上げられて懐かしい。この本が面白いと感じられたら将来の理系間違いなし?
- ケーニヒスベルクの橋渡り
- 一筆書き問題(一筆書きができる条件。何かの実世界の問題で解説してびっくりされた微かな記憶)
- ニセモノ金貨を入れた袋
- エラー訂正のページで紹介したコロンボの偽金貨問題(初めて読んだのはこのアラブの商人さん設定でした)
- 2すみを切り落としたチェスの盤
- 想定している小学校で読んだ本ではないかもしれないがどこかで読んだ
- 正直な部族とうそつきな部族
- これもどこで最初に読んだかはっきりしないけど
- 機関車のすれ違い
- 設定若干違うが原理同じ。
- 効率的な分銅の決め方
- 出典ちと自信ないが
- 最短の道のりでかける橋
- ちょっと設定が違う問題だったきがするが、原理は同じ
- 円形でない丸太のコロ
- マツダのロータリーエンジン? 中学の技術の時間に思い出して感銘
- 3組の夫婦の川渡
- 変形で二人きりにしてはいけない組み合わせ(キツネか狼と、鶏とか)がある川渡しだったきはする
記憶と微妙に違う似た問題あるきはするけど、でもいつ見たのが最初かはっきりしない結論として懐かしく面白い問題もいっぱいあります。
暇つぶしに数学に興味があったらお勧めします。
摩訶不思議な第一問: 正方形がある。各辺に任意の一点選んで、その4点から、最初の正方形を再現できるか?という問題です。
(2018.04.09)new3流の解答は、任意点の選び方によって、再現できる場合もあるが、正方形を描くことができるが、条件により(複数描ける正方形の)どれが最初の正方形か判断できないこともある。
まあ、名作パズルには値しない気がする。
a)正方形の向き合う辺に対して水平な線による交点と、垂直な線による交点を選んだ場合(向かい合う点を結んだ線分は、互いに直行する場合であり、なおかつ、復元時にこの条件で選ばれた点であることを、認知している場合) → 線分で分けられた4つの三角形をそれぞれ回転対称と重ねて生成する長方形4つの作るものが元の正方形。 ⇒下記2)の、正方形A'B'C'Dに対して、abcdを残す点として選んだ場合、三角形cdoに対して、cdD’を拡張して、同様に、A',B',C'を作図し、正方形A'B'C'Dを再現できる。
b)向き合う残点を結んだac,bdが直行する場合およびa)の元正方形の辺と水平垂直な関係であるが、水平垂直な関係だったと意識しないで再現する場合。
正方形を描くことは可能であるが、最初の正方形と同じものかどうかを判断することはできない。
向き合う2点をそれぞれ通る平行線を描く(残る2点を結ぶ線分と交差、接触しなければok)。 次に、残る2点から、この平行線に垂線を下してできる交点を結んだ正方形も必要条件を満足するが、十分条件を満足しない。
c)上記a),b)に該当しない(対向する点を結んだ線分が、互いに直行しない)場合、本書の解法で、もとの正方形を再現できる。
元の正方形が再現できない条件をうまく表現できないので、名作パズルとよぶ価値ないんじゃないかな? 対向する2点をそれぞれ結んだ線分が直行すると、解が決まらないという表現は簡単であるが、この表現を示すと、問題解法の重要なヒントとなってしまうので、名作と呼ぶには値しない。
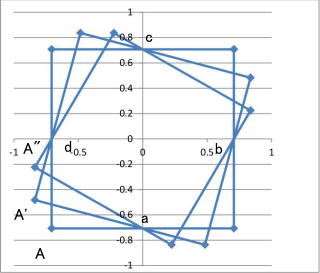
(2018.04.10)パズルとして例外が残念というのは確かだけど、アイデアは生かして、元の正方形を再現できるか?ではなく、この4点を通る正方形を作図せよという問題にすれば名作に値するかも。例題は直行しない図を示して、応用例として、正方形の頂点から別の正方形を生み出す例(↓1のabcdからA,A'等の正方形を示す) )と、不規則に直行する例2)を示して、実は、回答は一つとは限らないというのをさらに示すと、興味がわく気がする
直行する場合、交差しない条件で任意の平行線を描いて、作図できますが、直行しない場合は、第五のポイントを推定できるので、任意の平行線ではなく特定の平行線を引くことができるので、最初の正方形を復元できるという意味かと思います。 本で問題を見て、なにか条件が足りない(その追加条件は何?)という第一観は案外正しかったのかな(頭の中ではわかりやすい想定:直行する例で考えていたので、特にそうだったのかもしれません。4つの円の四角形内部での交点とか、交わり有無、等から、第五の条件かと思ったけど、本屋立ち読みでは目途が立たず、購入する羽目になりました。
---------初期検討の内容------------
立ち読みで考えた第一感は、残された4点を頂点とする(不等辺)四角形をまず書いて、次に、各辺を直径とする円を書く(とりあえず四角形の外側の半円に注目)。復習のために、円周角を思い出してください。直径を一辺とし、もう一点円周上の点を結ぶ三角形は、どの位置でも直角三角形になります。 言い換えると、この(半)円周上に復元したいもとの頂点(90度の)があります。そして、この点から、直径と円の交点をとおって、隣の円周上の点を結んで行って同様に作図をつづけ、右回り作図と、左回り作図が、最後に交わって、長方形ができて(必要条件の一つ)、さらに長さが等しくなる(必要条件、直行する任意の二線で十分)解があるかどうか?という問題だと思いました。
大きな直径の円から始めると線が引きにくい(交点ができない場合が多い)気はするが、小さい円から始めると、線が引けるきがした(4つの円の四角形の中側の交点とか中点がポイントかと思ったけど、立ち読み頭の中の検討ではわからず解答編を眺めてみる)。
(2018.04.02再改定)正解は、(詳細は本を読んでください)残点として選ばれた4点で構成される四角形の対角線をまず引いて、ある補助線を引いて解を求めるというものですが、偶然対角線が、直行した場合には、補助線が引けないので、書籍の解が使えない(示された解答は十分では無い)。解は無限個ある しかしこの偶然直行の場合、2つの場合が存在し、非直行で3つの分類が出来そう。 はかったような対称波形で直行する対角線の下記1)の場合や、ちょっと偏った気がする2)のA'B'C'D'に対するabcd点選択の場合だけでなく、下記2)のABCDに対するabcdのような一見ランダムな(でも偶然直行している)ような図形ですら、一義的に解がきまらないというのは、パズルとしてはいかがなものかという不平を述べて本件検討の結果としたい。
1)2つの対抗線が互いに垂直二等分線になる場合。例えば、4点がもとの辺の中点だった場合(正方形Aに対してa,b,c,dを残点として選んだ場合)。
正方形の重心(中点の対角線が交わるところ)を中心に回転し、最初に定めた4点を通るように、リサイズすると、定めた4点を通る大きさの違う正方形が無制限に作成できる。逆にいうと、定められた4点を通る四角形は一つに決まらない。正方形Aに対して、各辺の中点を、a,b,c,dとする。この4点を通る正方形A',A"等相似形が無限に生成することができる。ちなみに、正方形abcdが、各辺の中の1点という条件から外れるが、極限の解。

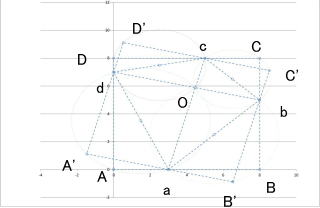
2)偶然直行する場合(2等分線にはならない)。 ABCDという正方形に、適当に対角線acを引いて、これと直行するbdをまた適当に引いた場合(その交点をOとする)。選ばれた4点からなる不等辺四角形は、対角線により4つの直角三角形に分割される。それぞれの三角形の回転対称な三角形を加えて長方形を作る(たとえば三角形aOdに対して、回転対称のaA'dを作図合成し長方形A'aOdを生成。同様に合成する4つの長方形を合成(A'B'C'D')すると、正方形となる(直行する対角線はもと図形が正方形なら長さが等しいのでできた合成四角形は正方形)。ただしもとのABCD正方形とは、一辺の長さが異なり、相似であっても合同ではない(一意に図形がきまらない)。 ↓の図はエクセルの作図でXY長さが合わないのでひし形に見えるが、座標を元に計算してみてください。直角が確保されているのが解るはずです。
この場合も、たとえば、a点を選んで、これを通る任意の直線を引く。次に点cを通りこの線と平行な直線を引く(2つの平行線が、有限長の線分b,dと交差・接触しなければok)。点bとdから、この並行2線に垂線を引く。4線が交点できたものが、点abcdを通る正方形の一つ。最初のa点を通る直線の角度により無限の解ができる。
| 元正方形 | x | y | 任意点 | x | y | |
| A | 0 | 0 | a | 3 | 0 | |
| B | 8 | 0 | b | 8 | 5 | |
| C | 8 | 8 | c | 5 | 8 | |
| D | 0 | 8 | d | 0 | 7 |
| 別正方形 | x | y |
| A' | -1.470588235 | 1.117647059 |
| B' | 6.529411765 | -0.882352941 |
| C' | 8.529411765 | 7.117647059 |
| D' | 0.529411765 | 9.117647059 |
しかしながら、この例でいうと、任意に決めた4点の対角線が、もとの正方形と平行である場合:つまり上記例のA',B',C',D'という正方形がまずあって、abcdを選んだら、A'D'//ac//B'C'かつA'B'//db//C'D'の条件を選んだ時、abcdを通る正方形の別解ABCDをえる方法がわからなかったりする。
一意に定まらないとはいえ、選ばれた点から一片を引くところからスタートという意味では(直行しない場合は解一つで、直行した場合は解が無限)、同様な解釈の範疇ともいえる。 直行する場合と、しない場合の二つの解というのは、結局たいして面白いパズルではなかったかも
3)それ以外の場合(対角線が直行しない)。 確かに本書の解答例が、正方形の生成方法であるのはわかる。だがこれ一つが解なのか?複数解の一つなのか、もやもやしている状態。
講談社に、”1),2)がおかしいやん”文句言おうかとおもったけど、3)の別解有る無しがまだすっきりしないので悩んでいる途中。本屋で立ち読みのとき、円を描くという想像から、解が2つあってもおかしくないというのが第一観で、場合により一つに決まらないのはわかったがまだすっきりできてない。二次式の解が、重根が3)で、虚根が1)と,2)に相当する?(虚根の解釈はもやもや)。 3)が重根(一つしか解がない)ではなく、二重解が普通なのではないか? ラズパイに、マセマチカという数理処理ソフトがはいっているので、これを使って方程式説かせようかと算段中(二次式なので面倒で手計算で解く気が失せる。最初の正方形の長さは代表値で(たとえば1に決めて)よいとして、四辺の中の、4点abcdの座標は変数で、変数多すぎ)。円周上にA点(x0,y0)の任意の点を選んだ時、この直径を通る2つの直線を引いて、となりの円周との交点を、B点(x1,y1)と、C点(x2,y2)とすると、最初のA点(x0,y0)との距離をLb、Lcとして、Lb=LcとなるA点を求めるのが、最初の条件。次に、B点C点からとなりの円周の四辺形の外側に交点がとれるかどうかが二つ目の条件のはずです。
雑談:偶然ですが、著者は、情報工学課の公開授業でお世話になった先生でした(名前の発音に濁音が入るのが珍しくて記憶に残っている先生)。
何を教わったかというとそれほど自信がないけど
・フォートランの実習(終わりの頃の講義ではTSR80という8ビットマイコンをミニコン?端末としてLANでつないで、フォートランのプログラム入力および実行のデモを見せてもらう。マークシートの紙カードにマークして、一束の紙カードデックを使って、プログラム実習してたのから考えてちょっと驚き。 教養学部のときには、オキタックというミニコンを数学課先輩に触らせてもらいましたがやはりカードデック。4年で研究室配属になったころ、8ビットマイコンにCP/MというOSをいれると、マイクロソフトのフォートラン80(77かな?)という処理系が使えるので驚き。 紙カード→オンライン端末→スタンドアローン :マイコン/PCの進歩って早いなぁ)。知り合いの修士論文はMSDOS上のフォートラン80使っていたような...研究室配属になったころその研究室は数値計算による研究がメインだったのに、知らない間に、マイコンによる教育効率アップ(コンピュータ エイディッド エディュケーション)みたいなまるで違う分野が主戦場に変わってちょっと(@_@;)。 フォートランって継続行のしるしは何文字目だとか形式ばった書式きらいで、BASIC言語の柔軟性にもろ手を挙げて賛同。C言語も関数の塊でそれぞれ宣言とか多く面倒だと思っていたけど、職場先輩は、さらに厳格なPascal派。あの書式やだったなぁ
・ゲーム理論(決してドラクエとかマリオに関係ありません。問題解決するのに、どのようにリソース割り振ると効率よいか?という作戦論?)。結構パズルっぽくて楽しかった記憶はある。そういう意味でいうと、この先生数学パズルと縁がなかったわけではない気はする。
あたりだったんじゃないかな?情報工学概論というようなものだったかなぁ?
サイトマップ 、トップ <*> (熊さんの色は , 変な立体)