R2R ラダーDAC
2017.1.1
サイトマップ 、トップ << 電よも < < テブナンの定理
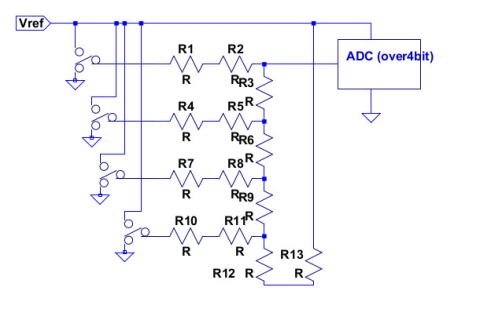
簡単に出力ポートの2進数(ストレートバイナリ)を、アナログに変換するには、R2R抵抗ラダーが簡単です。
動作の理解には、All0(全ビット0)の場合がまず簡単です。
All0の場合、出力は、0です。この場合の合成抵抗を考えてみましょう。LSBも2ndLSBもL出力です。したがって、bit0,1の抵抗出力の交点は、2Rの抵抗がGNDに、並列につながっています。したがって、抵抗値R。このRが、ビット1-2のRと直列の2Rとなります。これと、bit2の2RがGNDに並行接続となるので、やはりR。これがbit2-3のRと直列なのでやはり合成2R。..最後の出力抵抗はRになる算段です。
ところで電圧は、2つの入力端子の電圧の中間値につながった合成抵抗Rになります。これが隣接ビット接続Rと合成され2Rの(Va+Vb)/2電圧につながった合成抵抗2Rとして、次段につながっていきます。 各ビットの出力は0かVだとします。するとビット毎のon/offをbnで表すとると、
Vout=V*(b7/2+b6/4+b5/8+b4/16+b3/32+b2/32+b1/64+b0/128) の電源につながった合成抵抗Rとなります。 図入りの解説みつけたので、リンクしておきます
この応用として、マイコンの入力ポートに複数のデータを与える場合、もちろん、そのポートの数入力ピンがあれば、問題ありません。
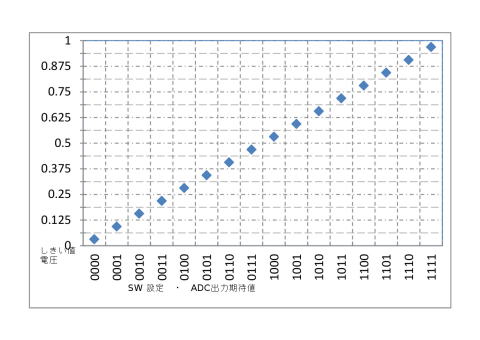
余っているADCのポートがある場合、その1ポートで、例えば4ビット(16通りの)設定を与えたい場合、R2R方式のDACで電圧を与え、マイコンがAD変換するというのが、便利だったりします。 回路的には5ビットポートでLSBが固定”H”になっている回路にすると、ADC変換値は、
1/2のオフセットがつくため、±1/2未満の誤差は、単に切り捨て(上位ビットのみ利用)することで、簡単にデータを判断することができます。
このオフセットがない場合、例えば”0100”の設定をしたかった時、”0011.10”、”0100.0”、”0100.01”を読み取る可能性があるので、ソフトで、四捨五入の処理が必要になります。 一方、このオフセットがあれば、”0100.1*”、”0100.0*”の4通りがあっても、切り捨てるだけの処理で判定可能です。


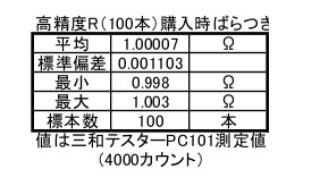
この方式で16ビットのR2Rを作るために、1kΩ選別品100本の抵抗を日本橋の某パーツショップで購入してみました。
まあ、偶然ですが、下位15ビットまでは単調性が確保できていました。7FFF→8000に変化するときだけ、アナログ値は、増加せず、わずかですが、値が減少するという単調性が崩れる問題が発生しました。最悪同じなら目をつぶったのですけどネ。残念。単純にいうと、ビット14-0の合成抵抗2Rが、ビット15の2Rより小さいことが問題であるので、R15関連抵抗を小さいものに試行錯誤しながら何回か置き換えて、なんとか、単調性が得られました(抵抗はサンプル数が一番多い1.000k表示になったものから、取り出し時値がぶれない物を選択。
あくまで、単なる偶然の結果ですが、100本の抵抗値の、手持ちテスターPC101による測定値の分布は優秀だと思います。テスターがあと一ケタ有効数字があると、もっと正規分布らしいのかどうなのか、わかるかもしれません。まあ、サンプル1袋分だけの結果でどうこういってもあれでしょうね。メーカ出荷ではなく店舗選別だったりするとばらつき大きいかな?(メーカ出荷高精度版を単に袋詰めかな?)
まあ、テスター買い換える気はないなぁ(温度計オプションがあるのですが、シリアル通信でテスターとつないだPCの専用ソフトでないと温度が解らない不満はある。 でXPのPCがお隠れになって、FDから他のPCにインストールしようとしたらFDが読めない。..バックアップ取ってなかったのが失敗。最新版ソフトは既にこのモデル非対応なのが悲しい(RS232Cというのがすでに過去のものなんでしょう)。いろいろなRS232のUSB変換器手元にあるので、FDが読めれば試してみたいが、ダメもとで新しいバージョンのソフトはちと買うのは無駄になると悲しい、熱電対の特性でも調べて使う方法でも考えようかという気はするが、長時間データロガーとしてももう利用すること無さそうなので、放置が妥当かな)

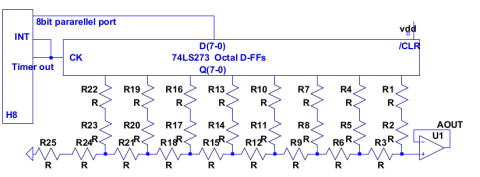
ちなみに、16ビットDACは、H8マイコンで、DDSにより、AM,FM、PWM幅変調機能つきのパターンジェネレータ:SGを作ろうとしましたが、掛け算が遅いというのも大きな欠点で、100kHzすら限界。ゲイン調整あきらめて、ROMデータそのまま出す仮仕様ならいちおうMHz台でるのですが、保留中。ARMプロセッサでやり直す予定です。 FPGAかな? FPGAならΣΔDACもありかな?(帰還はデジタル領域でやれば、DCオフセットついちゃいますが、それなりに動くかも。 下記は図を書くのが面倒なので8ビット分のみ作図した例。ちなみに、Rと2Rという2値の抵抗持ってくればシンプルな回路になりますが、違う規格(値)の違う抵抗間で精度が良いわけないので、パラレル抵抗にして半分の抵抗値のものをつくるか、下記のように、直列抵抗で2倍の抵抗作る方が、無難だとおもいます。事実15ビットでよければ、単調性確保したラダー抵抗を実現できました。

とこりで、DACの単調性が崩れるというので思い出すのが、セットのプログラマブルCの調整が困ったこと。
数ビットの2のべき乗容量のコンデンサをプログラムで選んだものの合計値の調整可能コンデンサを用意していました。これと外付けL等とともに共振回路を生成して、回路にパルスを投入した後の自励共振の周期を測って周波数をモニタする仕組みがありました。


適当なパルスを印可しても、自励共振が発生している。

コンデンサの値を変えると共振周波数が変化するのが理解できる。

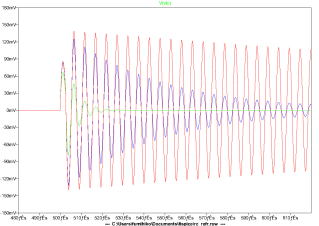
Qを変えるために並列抵抗の値を変えた。発振継続状況が変わるのが解る。
並列共振回路の並列Rなので大きいほうがQが高い。Qが低いとすぐ発信が止まるので測定困難。
周期は変化しないので、小信号でもよければ、しばらくは計測できるが。
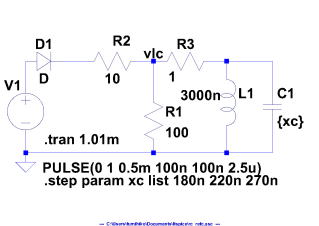
LC並列共振回路に、ダイオードで、パルスを印可した場合のシミュレーション。
C=220nF,L=3μHの場合:f=1/(2π√(LC))≒200kHz (周期約5μ)の自励共振がしばらく続くことがわかる。 この発信が止まらない間に周期の平均値を、求めれば共振周波数を推定することができる。Lを3μ(3u)と入力すると、2バイト文字μになるのですが、結果表示の画面で2バイト文字ばけるので、あえて3000nHとしています(アップデートしてみようかな)。 外部から周波数掃引して電圧を測れば、共振周波数を測ることができますが、こっちの方がお手軽だと言えます。 R1/R3の抵抗は、共振Qを決めるファクターで、定性的にいうと、どれだけ共振しやすいか(共振が継続しやすいか)を変えます。 まあ、そのうち、別途説明しましょう。
周波数から調整プログラムを作っていてうまくいかないものがある。調べると、例えば、 C5 < C4+C3+C2+C1+C0 になるばらつきがあるのが原因でした(周波数が高いので、コンデンサの量を増やすのに、上の例でいえば、修正前(C4+C3+C2+C1+C0)に、C0相当を加えたつもりの修正後(C5)にしたら、実際は容量が小さくなるので、さらに周波数が高くなってしまい、うまくいかないという例でした。
プログラマブルコンデンサは単調性保証しないと部品メーカがのたまうので、嫌味で、容量推定をしてみます。最小二乗法を久しぶりに使った例の一つ。
さて、周波数から、コンデンサ値の推定なのですが、この次元では計算がややこしい(ルートや逆数やらいろいろ面倒)。
そこで、計測Cの値を、実測した周期の逆数と、外付けLの値は、代表値と扱い、周期から測る共振周波数から、演算した求めたC値を、プログラムして足し算して合成されたC値として求めます(C=1/ω^2L 正確にいうとLが推定値なので、あくまで、C比例値の推定になりますが、大小比較という意味では十分です)。
コンデンサは、簡単な例として、2値のプログラマブルC1,C0と、基板等固定Cf。スイッチをX1,X0とします(オンを1、オフを0の2値)。
C = C1*X1 + C0*X0 +Cf
で計算できます。これより3元1次方程式の最小二乗法の解説になります。ルートも二乗も逆数も出てこないスマートな方程式の解法。力づくではなく、スマートな方法考えましょう。
誤差 E= C-(C1*X1 + C0*X0 +Cf)
二乗誤差 E^2 = (C-C1*X1 - C0*X0 -Cf)^2 ;誤差の正負考えるのが面倒なので2乗するのが定法なのです。
最小二乗誤差は、上記E^2を最小にするC1,C0,Cfを求めることになります。3つの求めたい容量で偏微分して、
∂(E^2)/∂C1 = ∂(E^2)/∂C2 = ∂(E^2)/∂Cf = 0 の連立方程式を解くことになります。
∂(E^2)/∂C1= 2* ∂E/∂C1 * E = -2*X1*(C-C1*X1 - C0*X0 -Cf)
= -2*(X1*C -C1X1^2-C0*X1*X0-Cf*X1)=0
→ C*X1 = C1*X1^2 +C0*X1*X0 + Cf*X1
∂(E^2)/∂C0= 2 * ∂E/∂C0 * E= -2*X0*(C-C1*X1 - C0*X0 -Cf)
= -2*(X0*C -C1*X1*X0-C0*X0^2-Cf*X0)=0
→ C*X0 = C1*X1*X0 +C0*X0^2 + Cf*X0
∂(E^2)/∂Cf= 2 * ∂E/∂Cf * E= -2*(C-C1*X1 - C0*X0 -Cf)
= -2*(C -C1*X1-C0*X0-Cf*1)=0
→ C = C1*X1 +C0*X0 + Cf*X1
統計処理に全データ集計するので、添え字iのサンプルデータをすべて総和をとる。測定誤差がでるので、複数回測定した結果から推定することになります。
→ Σ(Ci*X1i) = C1*Σ(X1i^2) +C0*Σ(X1i*X0i) + Cf*Σ(X1i)
→ Σ(Ci*X0i) = C1*Σ(X1i*X0i) +C0*Σ(X0i^2) + Cf*Σ(Xi0)
→ Σ(Ci) = C1*Σ(X1i) +C0*Σ(X0i) + Cf*Σ(1) ;Σ(1) は測定総数
誤差二乗の偏微分方程式として求めた上記の3方程式は、物理的に意味のわかる式になっています。最小二乗法から離れて3つのコンデンサの値を求める方程式を立てようとすると、妥当な式だと解る(もちろんほかの式を考える可能性もあるが変形すればこの形に収まるのでは?)。 両方のアプローチで考えてみるといいかも。
これを、C1,C0,Cfの3元一次方程式として解けば、良い。エクセルで逆行列求められたはずだが、今回なぜだかわからんが、うまくいかないので、前出サイトの公式で計算してみた。 実試行の時は旧excel(office xp)上で5~6元方程式手を解いたはずないので(手計算なんて端から考えてなく)'逆行列で解けた気がすが、(excell2010)で今回解を求めるのに、ほぼ半日行列式と格闘してあきらめました。
ちなみに結果はメーカ保証しないだけあって繰り上がりで単調性ずれるものがある(個体不良?メーカ出荷スペックとしては正常と言い張る)のが確認できたが、できることが価値があり最小最大リニアリティ等あまり期待していなとはいえ、スペックの有無とは別にして、単調性だけは、メーカの良心として何とかするもんじゃないか?と思う。
下記はc1,c2の目標値を決めて、各サンプルごとにそれぞれに±5%誤差をれて、オンオフ組み合わせを変え計算して求めたCの値32個から、最小二乗法を適応した場合の推定値。 まあ、こんなもんかな?
右下のCの数値とon/offスイッチの単純な数値からこんな分析が可能です。


数学って、便利なものというの実感できませんか?
------------------------------------------
サイトマップ 、トップ << 電よも < < テブナンの定理