アナログテスターの抵抗測定と
鳳・テブナンの定理
2017.1.1
サイトマップ 、トップ << Z < < テスターのC測定と過渡解析 <*> R2R ラダーDAC
まず、テスター内部抵抗は?という別スレで提示した問題です。
解放電圧Vopenが、1.54[V]でした。別のテスターで測って220Ωの抵抗Routをこのアナログテスターで測定すると、この抵抗両端の電圧Vrは、0.145[V]でした。 出力抵抗Rinはいくらか? 直列抵抗Routと、Vrに流れる電流は同じ。Vrにかかる電圧は(Vopen-Vr)ですね?だから、
Rin = (Vout-Vr)/Iout
=(Vout-Vr)/(Vr/Rout)
→本例 約2.1kΩ
では、148Ωつないで、0.102Vなら、→約2.1kΩ 3桁目誤差がでますが、まあこんなんかな?
さて、68Ωで1.11Vなら →26Ω? なぜ違う?? いや失礼、抵抗測定レンジが100倍違う例でした。概算として抵抗が1/100オーダですね(手抜きで零Ω調整してないので誤差大きいかも)
さて、学生時代に抵抗に関する演習問題で、テブナンの定理と名前が付くものを解きました。
初見の問題は、”内部電池Eiと抵抗rの直列回路iが、片側GND、もう一方が、オープン状態。このオープン端子とGNDの間に抵抗Roを接続したら、電流Ioが流れた。 直列抵抗rを求めよ。” なぜ、この問題を覚えていたかというと、上の単純な設問方式だとオームの法則の演習の単純バリエーションにすぎないのに、”定理”という枕詞までつけて”テブナンの定理”というタイトルが付いていたので、気になっていたということです。 ブラックボックスの等価回路扱いという考えを見直しました。さらに、その後、交流抵抗(インピーダンス)の問題として、再会し、拡張性に納得。鳳秀太郎先生偉い!ととりあえず褒めておきましょうか(年代調べるとやはりテブナンさんほめるべきかな)。
さて、テスターの抵抗測定の内部抵抗を求めるのは、(手持ちは偶然黒いテスタという)ブラックボックスの開放電圧と、決まった抵抗をつないだ場合の電圧(から抵抗Rの電流を計算すると流れる電流が求まる)→等価内部直列抵抗が推定できる。
まさにテブナンの定理演習問題そのままの話になります。 解法は難しくないし定理の名前知らなくても困らないけど、ブラックボックスの内部インピーダンスが計算できると言う論理のながれは、覚えておいて決して無駄になる事はないと思います。今回は直流なので、簡単な話になります。細かく言うと電流計は、分流器(抵抗)が並列になっているはず(レンジ切り替えで計測可能な電流以上のものは、並列にならんだ値を選んだ分流器抵抗に逃がし計器には一定範囲の電流を流して、値を換算して表示する)ですが、ブラックボックスとして。電流計計器と直列抵抗の単純回路(レンジで抵抗値が変わるだけ)という等価回路が、考えるうえで非常に便利なことがわかるでしょう。
後、充電池(ニッカドでもニッケル水素でも)って、だんだん悪くなりますね。 充電した直後テスターで測ると電圧ちゃんとあるのに、実際に使うとあっというまに動かなくなるという体験ありませんか? 理由は簡単で、電池の出力抵抗が劣化して大きくなる。この抵抗での電圧ドロップがロスになり電流流さない解放電圧はきちんと充電できたはずなのに、実際に使えないという寿命が発生するわけです。
最近入手した中古アナログテスターには、オンラインで取説読んでみると電池チェックモードというのがあって、負荷をかけて、電圧の合否判定しているそうです。 もし、テスター以外に、電池チェッカを持っていたら、電池の解法電圧測定と、測定時の電圧をテスターで測り、インピーダンス計算してみましょう。区別できないけど、新しいものと古いもので、どの程度インピーダンスが劣化するか?考えてみると面白いかも。
まあ、電源に直列抵抗いれて、同様にインピーダンス推定すれば、チェッカの内部インピーダンスが独立して求まるかな? 抵抗をボリュームにしてどのくらい電池インピーダンス上がるとだめだと、チェッカメーカが考えているか、調べてみるのも面白いかも。
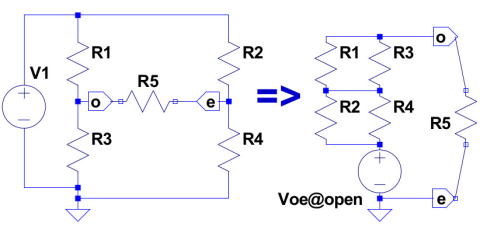
名前が付いているにはそれなりに理由があるんですよ(有難味がわかるのがいつだという保証は無いけどね)。 ついでなんで、面白い利用例として、4抵抗のブリッジ中点に抵抗を追加した場合の電流値の求め方。 R1とR3直列抵抗(接点をO点)と、R2とR4直列抵抗(接点をE点)の2組が電源に平行つながっている時、O接点と、E接点の間にR5をつないだ場合のR5の電流を求めるというもの。大学だと、平衡条件でR5に電流が流れないというのに注目して習うけど、実用上、平衡しない場合の動作解析が結構面倒だったりしますが、この定理を使うと、頭の中で解ける程度の問題なのが解ります(暗算苦手なので数値は電卓たたきますが、式は頭の中に浮かぶのが重要。 まあ頭の体操に考えてみて(ヒント:O接点電圧は抵抗比で判る。E接点電圧も同様。その差が、ブラックボックス開放時の出力電圧Voe。ブラックボックス内部抵抗は、O接点と、E接点をつかんで、(頭の中でトポロジー的に)引き伸ばしてみる。するとO点E点は、R1R3並列抵抗に、R2R4並列抵抗が直列につながった抵抗が繫がったように見えるはず。 さあここで、ブラックボックスオープン電圧Voeと、等価回路Roeが解りました。ここにR5抵抗つないだときの電流はいくらでしょうか?(回路網引き伸ばす時に電池がショート接続と考えるのがポイントです)。 電源の取り扱いが学生の時納得するのに時間がかかりましたが、なれれば簡単。 今この問題正攻法ならとキルヒホップの法則で、各ノードの電流和を使って方程式建てると思いますが、面倒です。とここまで書いて気が付いた。確かに似たような解析の演習問題をいくつも解いたような気がします(裏返し回路を作った等価回路の考え方に驚いたのは覚えているけど、うーん。 道具として使えるようには考え身についてないなぁ。未熟者)。

では、続きに雑談。
上記ブリッジ問題で電源でない場合どうでしょう? ICの出力がLになって、動作停止。Hになった場合のブリッジの例です。電源電圧としてみると、端子出力電圧=電源電圧Voとして同様に初期解放電圧を計算できます。がその後の等価回路抵抗0Ωとしてショートできません。抵抗rinを挟む別のブリッジができてしまうことになります。回路解くのは面倒だったりします。後は、物理常数が、等価的に、0と見なせるか、無視できないか?で解法が違うことになります。結局最初の乗数が平衡であっなら、この変形回路も平衡なので余計な電流流れないという話です。
実際具体的な、ICの出力インピーダンスは? たぶん仕様書書いてないかもしれませんね。 でも、例えば、10mAの駆動能力があるという記載があった場合は?この場合、10mA以上電流を引き込んでも、出力電圧が、Vthを超えないという解釈が一番簡単でしょう。10mAひっぱっても0.4V超えないという仮説だと、出力インピーダンスは、 Zout=(0.4)/10m=40Ω。 これが、大きな定数で等価回路のインピーダンスに影響するかしないかによって、そもそもの、R5という抵抗を挿入した場合に流れるが簡単に求まるか、誤差がでてくるのかに影響することになります。
物理的に解釈すると、無負荷時にVhという電圧が出力できるとして、R1~5の合成抵抗に電流を流すと、rinという出力抵抗でVhという電圧がでない(合成抵抗に流れる電流*rinの電圧ドロップが発生するという話だったりします。この電圧ドロップが、影響するかどうか?という話でしょう。まあ、あまり深く考えないように。
-------------------------------------------------------------------
サイトマップ 、トップ << Z < < テスターのC測定と過渡解析 <*> R2R ラダーDAC