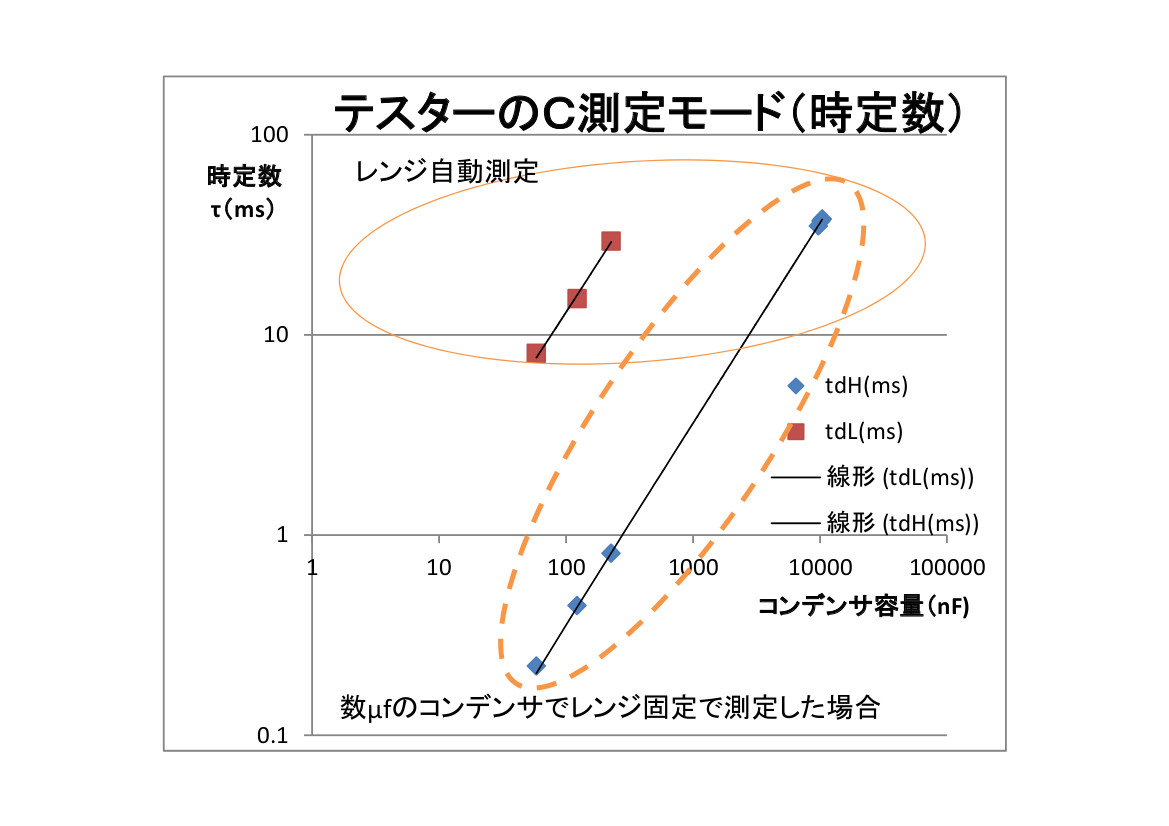
テスターのC(容量)測定と、過渡解析(ラプラス変換)
2017.1.13
サイトマップ 、トップ << Z < <*>アナログテスターの抵抗測定とテブナンの定理
前節で、テスターで抵抗値を測定することを解説しました。基本は、オームの法則 V=RI でしたね?
ところで、テスターの抵抗測定モードで、コンデンサを測定したことある人いますか? (Cの容量とテスタ本体の特性によりますが)針は一瞬ふれると思いますが、すぐ、オープン(抵抗値∞)になると思います。 それは、コンデンサとは、絶縁物を挟んだ平行電極なので、そもそも(直流)電流を流せない&電圧を加えると電極間が飽和するまで充電する(電荷が移動することができる。逆に電圧が下がると放電の電荷移動が発生する)ので、わずかながらも電流が流れる=針が振れるということです。
では、デジタルテスターでコンデンサを測る方法は? 簡単に想像できるのは、交流も測定できるんだから、電圧の決まった交流を加えて、電流を測定すれば、交流表示のオームの法則から抵抗値測定可能(交流抵抗は一般にインピーダンスと呼ばれます。実数ではなく複素数と考えるのが一般解釈かな?)。
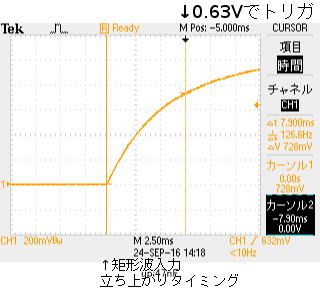
と、予想して、手持ちテスター(三和PC101)のC測定方法をオシロスコープで観察したら、なんとまあ、脈拍程度の矩形波(方形波)駆動。こんな低周波では電流流せないし、正弦波でないなら実効値換算しないと、電圧条件話が合わない。。道理でLをつなげて数値を補正すれば、L値が算出できるという予想がうまくいかない訳ですね。 まあ、正弦波という歪みのない交流を電池で動くテスターで作るのが面倒だという話なんでしょう。
たぶん他所で説明するけど、コンデンサのインピーダンス(抵抗みたなもの:交流抵抗:複素数)は、1/jωC (いっぽうコイルのそれはjωL)。
という訳で、交流駆動で、電流電圧関係からインピーダンスでCの値を算出しているなら、その読み取りC値(容量)をつかって、Lの値は、L=1/ω^2/C(テスター読み取り値)という計算ができると思ったのでした(普通位相は測定してないと勝手に予測)。
jは虚数単位で、”j^2 = -1”というよくわからん記号だけど、電気の世界でいうと、交流で考えて電流のピークと電圧のピークがその周波数の90度ずれにあるという意味になります。"1/j
= -j"ですが(分母・分子にjを掛ければわかります)、符号の意味は位相が進むのと遅れるのをこの符号で表します、まあ、忘れて良し。ちなみに、数学だと、”i”が使われますが、電気の世界で”i”は電流(電流密度)を示すのが公約なので、”j”と表記されます(と予想してみる)。
ω=2πf : 角速度。πは円周率 噂のゆとり教育だと3? 理系は少なくとも3.14くらいの有効数字は覚えておきましょうね。fは交流の周波数。円一周を360度ではなく、2πとする(ラジアンあるいは弧度(こど)という単位系:微積分を道具として使うようになるとこの単位系の有能性が分かるようになる、360は確かにいろんな数字で割れるので使い易いという面は認めます)と、1秒にどれくらいの角度動くかを示すので角速度といいます。直流でなく交流が前提。交流といえば、コンセントにきている商用電源が100Vで60Hzとか50Hz。国内で周波数が違うのはちと特殊(明治維新の頃、発電所をどこから買うかで話が違ってくる。統一してほしかったなぁ)。そもそも100Vというのも、世界の常識からいうとちょっと変らしい。最大電圧と実行電圧と当時理解していない誰かが勘違いして規格決めてない?と邪推してみる。海外旅行用品に電圧変換機器売ってるでしょ?交流の規格定義は機会があったらまた話しましょう。 ちなみに高校の頃かな正確なので電気時計というのを買いましたが、この頃は、自動でなく、手動で周波数切り替えてました(交流周波数を数えることで時間経度が選べるくらい日本の交流は安定して優秀です。外部業者参入許して将来の安定供給大丈夫なのか不安感じる)。正確なのはいいんだけど停電あると、ちとあたふたした。 グレムリンという映画で電気時計が結構重要なアイテムとして利用されていますが、覚えていますか?。 クリスマス時期にダイハード1/2とグレムリン、ホームアローン見るのが家の定番だったりします。いまのソーラ電波時計は素晴らしい(でも壊れやすい気が。10年で3機種のべ5台目利用中。最近買い替えたのは、バックアップ電池交換できるようになったので、寿命あるかも?)
πといえば、小学校の算数の授業で、グループで1枚レコード(LP)を学校にもっていって、布製の柔らかい巻き尺で、直径と、机の上を転がして円周長を測り円周率を測定。隣近所からは3.12だとか3.15だとかいう声が聞こえる中ぴったり3.14と割り切れたので喜んでいたら、先生に、3.14159...と続くので、3.14に割り切れても、優秀ではないと釘を刺された。mmメモリ小数点以下の読み取り値にしたので、まわりより精度良かったんかな? 有効数字とは大変重要なのよ>ゆとり世代の人へ
このC,Lのインピ-ダンス式で判るのは、(純)抵抗は直流でも直流でも普通に抵抗そのものだけど、LやCは周波数によって抵抗値(正確に言えばインピーダンス)が変わるという事。および電流と電圧に位相差があるという意味。
Lは直流で抵抗”0”Ω。まあ。単に電線くるくる巻いただけだから配線抵抗なんで0と近似で実用上いいでしょ? そして交流で周波数が高くなれば抵抗が大きくなって電流が流れないということ。チョークコイルというのはこの意味で目的周波数より高い波を通さない用途になります。昔のAMラジオ(中波ラジオ)のアンテナとして、(フェライトという誘電率の高い)黒い棒の周りに線をくるくるまいたものも”L”の応用例です。中学校の時買ってもらったナショナル(現パナソ)のクーガというAM/FM/短波のラジオは、このアンテナLを本体外部に引っ張り出して、本体と独立し(放送局の送信アンテナの)向きに角度を変えて、受信感度をアップでき便利でした(じゃまな近隣周波数からの漏れを小さくするという用途もあった気がします)。
Cは直流だと抵抗∞(電流は流れない)。単純にいえば、絶縁体を挟んだ金属板(現物はこの広い板をくるくる巻いて小さくする)だから、連続して電流流れるわけがありません。周波数が上がると抵抗値(インピーダンス)は下がり電流が流れやすい。またCの値は大きければ大きいほど抵抗値は下がる。 高周波ノイズをグランドに逃がしてしまうという方法なので、Lとはアプローチ違いますが、特に電源周りでノイズを軽減する道具としても使います。
先のアンテナの話に戻る。Lは単に存在するだけでも、ファラデーの法則で示される能力とか、フレミングの法則で示される向きで、電磁波を電気に変えることができます。 しかし効率を考えると、LC組み合わせ。インピーダンスは、LとCで、周波数特性が逆で、(位相)極性も逆。周波数を選ぶと、(L起因とC起因が逆向きなので打ち消しあう点で)インピーダンスが最小になる点があります。これが共振周波数。一番効率よく電波を取り込める(インピーダンスが低いので効率よく電流が流れやすい)周波数です。 逆に、LかCの値を変えると、共振周波数が変わるというわけです。 ラジオの選局は、普通Cの値をかえて、共振周波数を変えます(いまはシンセサイザーとか、原理がまったく違うようですが)。
話はテスターのC測定に戻る。取説に説明無いけれど、RC時定数によるτ測定と想定しました。時定数の物理的な解説につづく。
RC直列回路の矩形波駆動の過渡解析
原理的にはコンデンサの両端の電圧は、その容量Cとたまった電荷Q(t)を使うと
Q(t)=∫i(t)dt = C・Vc(t)
加えた電圧に比例した電荷が溜まるのがコンデンサ。同じ電圧で電荷が溜まる量をコンデンサの容量と定義します。コンデンサにたまる電荷というのは電流の流れた総量(過去から今に至る時間すべて)という定義です。
RとCの2つの素子の直列回路なので、印可電圧V(t)は2つの素子の両端にかかる電圧を加算したものに相当する。2つの素子に流れる電流は直列接続なので常時(どの時間も)同じです。
Vrc=Vr(t)+Vc(t)=R*i(t) + 1/C * Q(t) =R*i(t)+1/C*∫i(t)dt
これを解くのは参考書でも引っ張って似た問題探さないと自信がない。
ところが、資料を見ないと覚えてないというのは同じでも、表を見れば済むラプラス変換という応用数学があって、受動回路の過渡応答の解析には非常に有力です。十分遅いの0v期間の間にコンデンサが完全放電し終わっているという想定ができます(コンデンサの容量と抵抗値によるが、計器が測定できる精度の範囲ではこの想定が実現できているのが正しい:逆にいえば測定可能範囲を決める条件の一つ)。
で、0[v]→Vrc[v]atT=0のステップ応答"Vrc/s"の電源と考えてよく、RはR,コンデンサCは、1/sC、(今回関係ないけど、コイルはLs)というインピーダンスとして回路を解析すればよい。ついでに補足。充電はRC直列充電で、放電はRを介さない高速放電(ダイオードでも入っているんかな)みたい(単に立ち上がりと、立下りの駆動能力が違うだけという説もある))。時定数が長くなっても。急速放電で、0Vスタートさせて誤差を防いででいるようです。
Vrc/s = I(s)*R + 1/(s*C)*I(s) → I(s) = Vrc/(sR+1/C)=Vrc/(R(S+1/RC))
I(t)=逆ラプラス{Vrc/(R(S+1/RC))}=Vrc/R*e^(-t/(RC))
式の意味は、Vrcが印可された瞬間抵抗Rを介してVrc/Rの電流が流れて、時間とともに(コンデンサに充電されるにつれて)指数的に減少する事を示す。この最初の電流値は、電源Vrcを、抵抗Rに加えたときに流れる電流(最初の一瞬だけCがなかったかのような電流)。
つまり一瞬電流がながれて、直流的には電流流れないというよくわかる現象を示しています。
このネイピア数e :自然対数の底=2.718282828459045は、高校で理系ならご存知だと思います(オイラーとも関係する)。
この式の一番特異な状態は、(e^0は例外にして) e^(-1)=0.368だと思いませんか?つまり、-1=-t/(RC) が、特殊な状況と認識されていて
τ=RC :RC直列回路の時定数と呼ばれます。ここで便利なのでついでに計算すると、1-e^(-1)=0.632。
コンデンサにかかる電圧は
Vc=Vrc-Vr=Vrc-R*I(t)=Vrc-R*Vrc/R*e^(-t/(RC))=Vrc*(1-e^(-t/(RC)))
ここで、0V→1Vの入力電圧変化が起きたとき、コンデンサ両端電圧が0v→0.632*1vとなるまでの時間が時定数となります。
つまりこの時間と、直列抵抗値から、コンデンサの値Cが C=τ/R と求まるわけです。
念のため注意しておきます。
このテスターが、時定数の測定をしていると断言したわけではありません。電圧が1/2になる時間:V/2=e^(-0.6931)=e^(-t/(RC))を解いても同じです(換算式が微妙に違うだけ)。回路としては0.632になる時間を測るより、単純に駆動電圧の1/2になる時間測定回路(抵抗分圧基準電圧とのコンパレータ変化時間)を作る方が楽(回路精度が得やすい。傾きが高い部分を測定する方が誤差少ないし)。 時定数という概念・定義をお話しするのに適当なテーマなのでついでに触れてみました。 時定数といえば大学の制御工学の先生が体温計の高速測定法として話をしてくれたのが、水銀柱が温まって平衡状態になるまで待つ従来型に対して、常温から、わきにさした瞬間の傾きの差から、最終到達温度を予測する手法で高速体温計を作ると豪語しておりました。 その教授の流れなのか、ほかの人の努力なのか判りませんが今病院で体温測るとすぐ対応わかりますね。時定数というのは道具として便利なんですよ実に。
あと、テスターのプローブのみで測定した時と、下記測定のために、オシロスコーププローブをつけたときの、表示値が大きく異なる。そこがいまいち理解不能。たかだか、1M10pFの規格値のプローブつけても、SPICE演算だって、こんなに、差異でるわけないんだけどなぁ。 プローブ2本つける場合の変化を含めて、さらに暗夜行路。何分説明書にないこと試して、想像しているだけなので、ピント外れだったら申し訳ない。
あ、個人私物を勝手に遊んだ結果だけなので、これをもとに何かの設計につかうとか、テスターメーカさんに問い合わせるのは、だめよ。


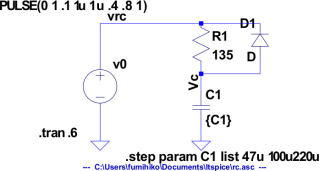
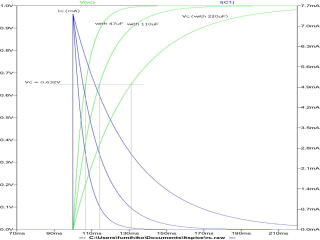
LTSPICEによるRC回路の時定数解析の例 コンデンサの値を47/100/220μFに変化させて、充電時間尾変異を見た。
オーダとしては、実測値とほぼ同等。
青色の電流が、一瞬最大値V/Rに達して、その後充電するにしたがって減少していくのがうかがえる。
R1にダイオードを入れたのは、立下りがコンデンサがついても比較的高速なので試しにいれてみた。
ラプラス変換のすすめ
正直数学の授業のラプラス変換はよくわからんかった。同時期に学んだのフーリエ変換は時間軸と周波数軸の対比が非常に面白かったけど。
その認識が一変したのが過渡解析応用。過渡解析は微積分方程式を解く正攻法で最初は習うんだけど、単元が変わるとラプラス変換による解法が説明される。
乱暴な言い方をすれば、時間積分が1/s 時間微分がS倍という魔法のような置き換えたをしたS領域で代数的に式を変形し、逆ラプラス変換することで時間軸の解が求まります。授業でこの応用に衝撃。 微積分の式を解くとき、初期条件がどうのこうの、、読んでも解るような解らないようなむずむず感が高かった(テキストの説明を意地悪く読むと、最終結果論がこうなるのが正しいので初期条件はこのようにするというごまかしがあるようで、気持ち悪い)。
この衝撃から回路解析演習の授業で、過渡解析の単元でも、ひねくれものの小生はラプラス変換を利用。 ある問題でテキストの微分方程式による解法の結果が、自分でラプラス変換で解いたものと結果が違う。 対称定数を選んだ場合振動しないはずなのに、テキスト回答例ではそれが出てこないので先生にクレーム。”物理的におかしい”という説明で納得してもらった。まあ、微積分法のどこがおかしいという間違いの指摘ができなかったのが自分の限界でした(今ならわかる。初期条件の定常電流の向きと、過渡解析中の過渡電流の向きが異なるので、符号を変えて式をたてなければいけない。本屋の流通版直っているけど、符号を変える理由の説明直観的では無いなぁ)。
後日談:”優”の実力無いと単位は与えないという方針なので日々小テストと定期テストで普通合格しないのという変な科目(電子工学専攻ならこれくらい解けるのが当たり前というのは正しい)。 この年は、上述のを含むテキストの微分方程式の章を、(出席番号順に割り振り)ラプラス変換で解きレポート提出。 さらに後日談:ラプラス変換で解いた問題集の新刊が書店店頭に並ぶ。おいおい。まあ今も手元で辞書(変換表)として活用中。
受動回路の過渡特性や伝達関数など電子回路・制御系初心者の君へ。
ラプラス変換の公式は有能。(原理や証明はともかく)変換・逆変換表の使い方を覚えるのは必須だと思いますよ。まあ、今は、LTスパイスとかPC上のソフトが無料でもいいものあるからねぇ。でも過渡解析はともかく伝達関数なんかこれ必須だと思う(偉そうに言っても、いまだにS領域とは何んだ?というのはもやもやと理解できず。でも道具と割り切ると便利です)。畳みこみとか重畳とかインパルス応答の意義関係が解れば合格。
SPICEの雑談。小生が入社した一年目に担当IC内部クロックドライバーの能力検証にSPICE利用。当時はオンラインUNIX端末でviテキストエディタで、回路接続情報(ネット)をテキスト入力。結果はラインプリンタの数値出力。数値上にラインマーカで数値を見ながら波形を書いて、見やすくするのを先輩から教わる。今の回路図・グラフ出力ベースのSPICEとは利便性が違う。いいなぁ。まあ、おかげで正規表現の使い方unix tools学べてよかった気はするが。 え?その検証結果はどうだったかって?(大きな見落としがあって量産性に大慌て。一年目だもん。うじうじ)。
CQ出版:LTspice入門編:神崎康宏
-------------------------------------------------------------------
サイトマップ 、トップ << Z < <*>アナログテスターの抵抗測定とテブナンの定理